Dependent Types
- General: Dependent types are type-valued functions.
- Specific: Functions that send terms to types.
Motivations
Vectors
Vector :: Nat -> *
init : Pi n : Nat . data -> Vector n
cons : Pi n : Nat . data -> Vector n -> Vector (n + 1)
Here, the $\Pi x : S.T$, or Pi x : S. T, is called "Pi type". This type generalizes the arrow type of the simply typed lambda-calculus. It is the type of functions which map elements $s:S$ to elements of $[x \mapsto s]T$.
Note the safe first:
first : Pi n : Nat . Vector (n + 1) -> data
We can use $\Pi x: S.T$ to generalize the function space $S \rightarrow T$, if x doesn't appear free in $T$.
Here, the stressing of being free is essentially saying that $T$'s formation has no relationship with $x:S$. Those, it degenerates to the simply typed case.
Another example
sprintf : Pi f : Format. Data(f) -> String
-- in which
Data([]) = Unit
Data("%d"::cs) = Nat * Data(cs)
Data("%s"::cs) = String * Data(cs)
-- ...
Curry-Howard correspondence
For example, $((A \rightarrow B) \rightarrow A) \rightarrow (A \rightarrow B) \rightarrow B$ is valid in constructive logic, and at the same time, is inhabited by term $\lambda f .\lambda u . u(f \, u)$.
If propositions are types, then proofs are terms.
A =====> B
| |
Prf A -> Prf B
CH-corres allows one to freely mix propositions and PL types.
ith : Pi n : Nat . Pi l : Nat . Lt(l, n) -> Vector(n) -> T
Here, Lt(l, n) is the proposition asserting that l is less then n.
Another example about the type of binary, associative operations on some type T:
Sigma m : T -> T -> T.
Pi x : T.
Pi y : T.
Pi z : T.
Id (m(x, m(y, z))) (m(m(x, y), z))
Here Sigma m : A . B(x) is the type of pairs where a : A and b: B(a).
Higher-Order Abstract Syntax
Ty :: *
Tm :: Ty -> *
base : Ty
arrow : Ty -> Ty -> Ty
app : Pi A : Ty . Pi B : Ty . Tm (arrow A B) -> Tm A -> Tm B
lam : Pi A : Ty . Pi B : Ty . (Tm A -> Tm B) -> Tm (arrow A B)
-- id on type A
idA = lam A A (\x : Tm A.x)
-- Church 2
two = \A:Ty. lam A (arrow (arrow A A) A)
(\x:Tm A.lam _ _
(\f:Tm (arrow A A).
app _ _ f (app _ _ f x)))
Pure First-Order Dependent Types
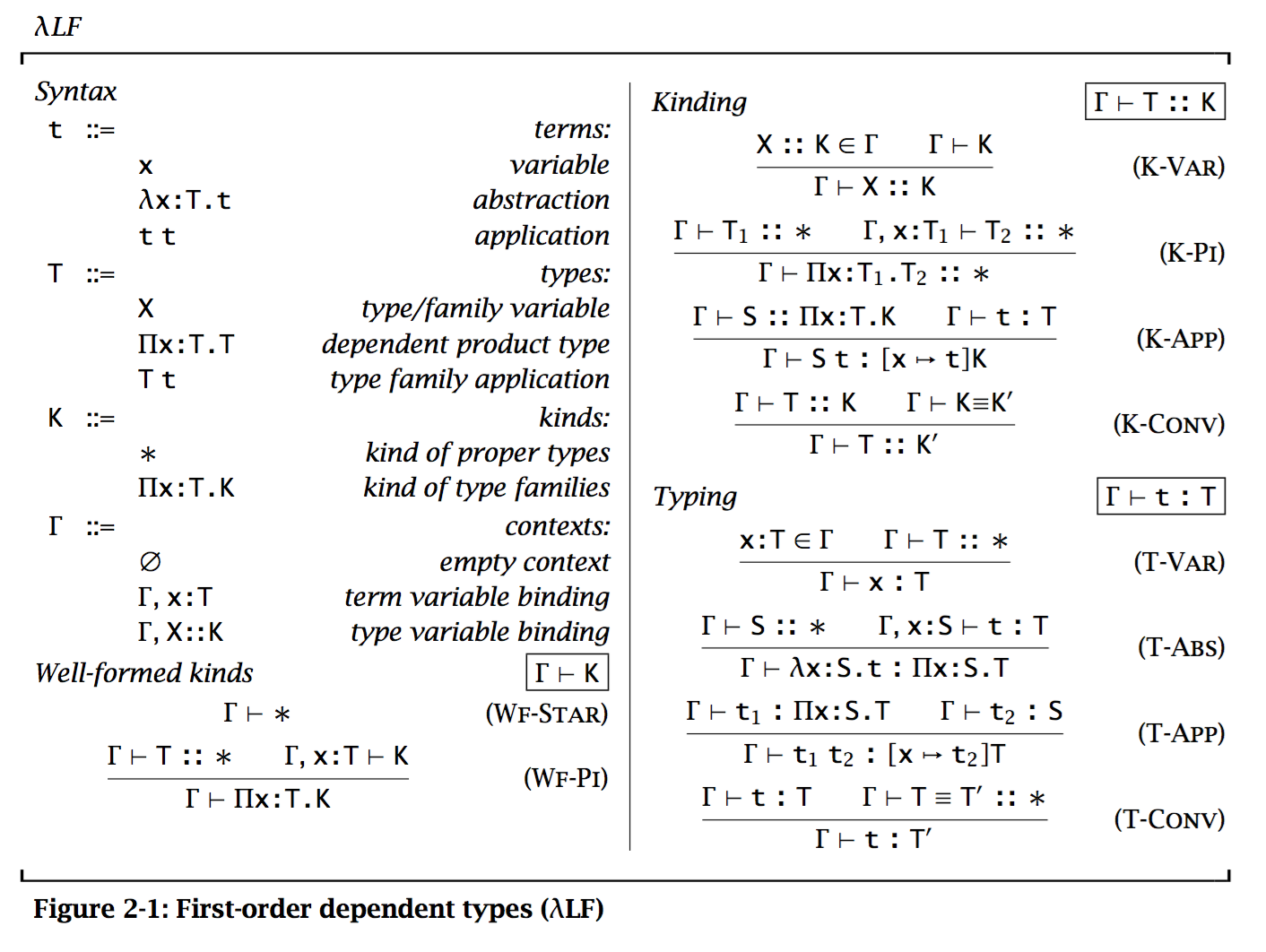
Kinds allow us to distinguish between proper types of kind * and type families if kind Pi x : T. K.
Problem introduces by type equivalence:
- Whether or not typechecking is decidable
Martin-Löf: definitional equality.