PPA - Intro
DFA
RDA
Reaching Definitions Analysis (or more properly, Reaching Assignment Analysis):
An assignment (or definition) of form
l: x := amay reach a certain program point if there is an execution of the program wherexwas last assigned a value oflwhen the point is reached.
So, $RD(l) = (RD_{entry}, RD_{exit})$, in which $RD_{entry}$ is the set of pair $(x, l_x)$ means that assignment to $x$ at line $l_x$ may reach $l$'s entry and likely for exit.
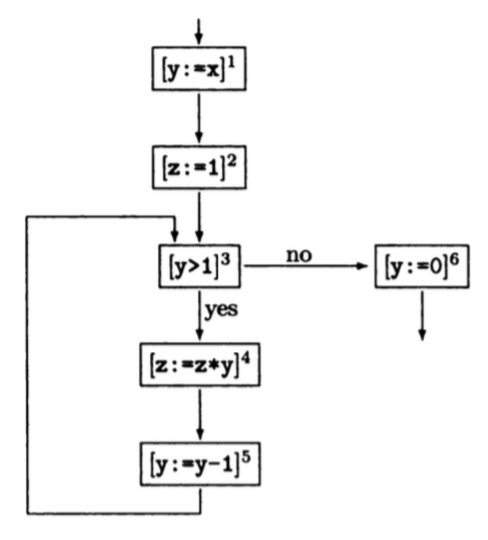
Exmaple:
1: y := x
2: z := 1
3: while y > 1 do
4: z := z * y
5: y := y - 1
6: y := 0
| $l$ | $RD_{entry}(l)$ | $RD_{exit}(l)$ |
|---|---|---|
| 1 | (x,?), (y,?), (z,?) | (x,?), (y,1), (z,?) |
| 2 | (x,?), (y,1), (z,?) | (x,?), (y,?), (z,2) |
| 3 | (x,?), (y,1), (y,5), (z,2), (z,4) | (x,?), (y,1), (y,5), (z,2), (z,4) |
| 4 | (x,?), (y,1), (y,5), (z,2), (z,4) | (x,?), (y,1), (y,5), (z,4) |
| 5 | (x,?), (y,1), (y,5), (z,4) | (x,?), (y,5), (z,4) |
| 6 | (x,?), (y,1), (y,5), (z,2), (z,4) | (x,?), (y,6), (z,2), (z,4) |
Equational Approach
Based on the flow information, we have two rules:
- For an assignment
l: x := a, we exclude all pairs $(x, l_0)$ from $RD_{entry}(l)$ and add $(x, l)$ to obtain $RD_{exit}(l)$; For non-assignment statement at $l$, $RD_{exit}(l) = RD_{entry}(l)$ - $RD_{entry}(l) = \cup_{i}RD_{exit}(l_i)$, in which $l_i \in$ all the labels from which control might pass to $l$; For the first statement, $RD_{entry}(1) = {(x, ?)\,|\, x \in Var}$
About least solution: The above system can be viewed as a function $F: [RD] \rightarrow [RD]$, which is a iterative process; so we can continue the process until reachability information doesn't change anymore, which is "least solution".
Constraint Approach
For an assignment l: z := a,
For non-assignment $l$, $RD_{exit}(l) \supseteq RD_{entry}(l)$
For any $l$, $RD_{entry}(l) \supseteq RD_{exit}(l_x)$ if $l_x$'s control might pass to $l$
And $RD_{entry}(1) \supseteq { (x, ?) \,|\, x \in Var}$
The "least solution" idea also applies to this method.