Global State
Global State $GS$ is
$GS$ is consistent iff C1 and C2 are satisfied:
- C1: $send(m_{ij}) \in LS_i \Rightarrow m_{ij} \in SC_{ij} \oplus rec(m_{ij}) \in LS_j$
- C2: $send(m_{ij}) \notin LS_i \Rightarrow m_{ij} \notin SC_{ij} \wedge rec(m_{ij}) \notin LS_j$
Note: $\oplus$ is exclusive-or
Every global state can be graphically represented by a cut in computation's space-time diagram.
Issues in recording a consistent global snapshot of a distributed system.
- I1: How to distinguish between the messages to be recorded in the snapshot (either in a channel state or a process state) from those not to be recorded?
- Any message that is sent by a process before recording its snapshot, must be recorded in the global snapshot (from C1).
- Any message that is sent by a process after recording its snapshot, must not be recorded in the global snapshot (from C2).
- How to determine the instant when a process takes its snapshot?
- A process $p_j$ must record its snapshot before processing a message $m_{ij}$ that was sent by process $p_i$ after recording its snapshot.
FIFO Snapshot algorithm
Chandy-Lamport Algorithm
- After a site has recorded its snapshot, it sends a marker along all of its outgoing channels before sending out any more messages
- A process must record its snapshot no later than when it receives a marker on any of its incoming channels.
Mark sending rule
- Process $p_i$ records its state
- For each outgoing channel $C$ on which a marker has not been sent, $p_i$ sends a marker along $C$ before $p_i$ sends further messages along $C$.
Mark receiving rule
On receiving a marker along channel $C$:
- If $p_j$ has not recorded its state
- Then
- record the state of $C$ as the empty set
- Execute the "marker sending rule"
- Else
- Record the state of $C$ as the set of messages received along $C$ after $p_{j}$'s last state recording and before this marker's receiving.
- Then
Understanding
The text from p96 to p97 is not very self-apparent. I think the topic is about the value of recorded snapshots in such a way.
Theorem: Exists $seq$'s permutation $seq'$ s.t. the recorded global state $S^$ is a middle-stop between $S_i$ and $S_t$, i.e. $S_i \rightarrow_{prefix(seq')} S^ \rightarrow_{seq' - prefix(seq')} S_t$. Here, $seq$ is sequences of events happened globally from $S_i$ to $S_t$.
The idea in this theorem is that, we can permute the order of events to "stretch" the diagram, in which the recorded state is a "real" state.
Definition:
- Pre-recording: A $e$ occurs on a process $p$ and $p$ records its state after $e$ in $seq$.
- Post-recording: A $e$ occurs on a process $p$ and $p$ records its state before $e$ in $seq$.
This definition is kind of anti-intuitive. "Post" and "pre" should describe the relative ordering of $e$ to recording.
Theorem: A post-recording event may occur after a pre-recording event only if the two events occur on different processes.
Theorem: A post-recording event can be swapped with an immediately following pre-recording event in a sequence without affecting the local states of either of the two processes on which the two events occur
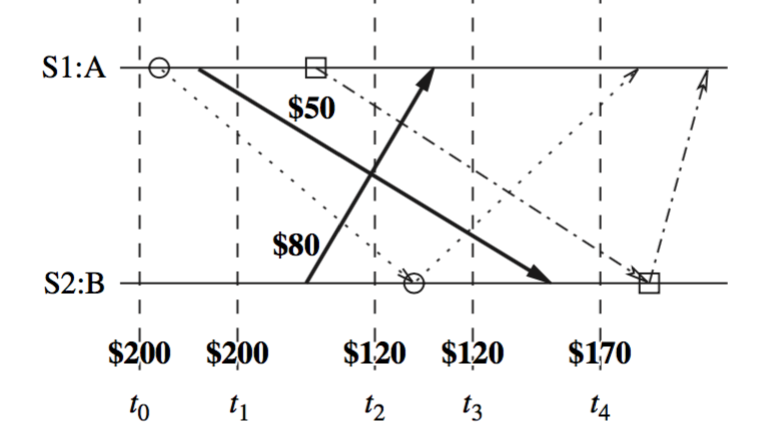
For this theorem, a example would be excellent.
Before swapping:
After swapping:
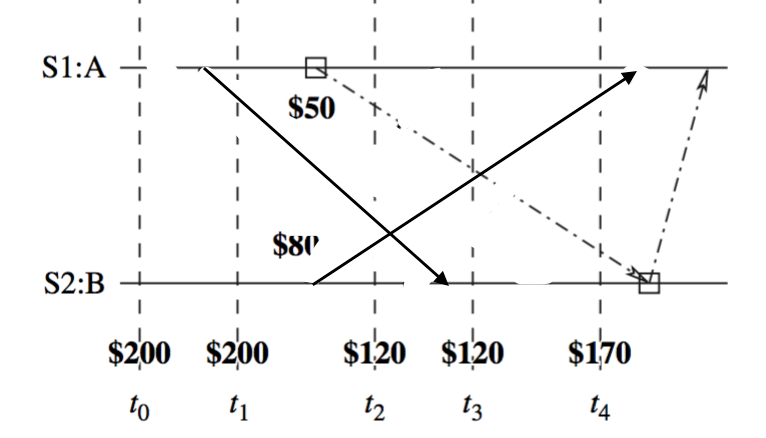
So you understand that:
A pre-recording one is made even earlier, while a post-recording one is made later.
Proof to first theorem: By iteratively applying the swapping operation, the permutation $seq'$ is obtained. So $S^*$ is the state after all the pre-recording events have been executed, but before any post-recording event.
Therefore, a recorded global state is useful in detecting stable properties.
non-FIFO Snapshot Algorithm
How to capture out-of-sequence messages to record a consistent global snapshot?
- Message Inhibition (Helary et al.)
- Piggybacking of computation messages (Lai-Yang et al.)
Message Inhibition
After marker is sent, only when a ack for marker is received, will other messages be sent.
Lai-Yang's Piggybacking algorithm
A coloring scheme. Two colors:
- Red
- Red process: A process having taken a snapshot and going to send markers
- Red message: A message sent by red process
- White
- White process: A process not yet taken a snapshot
- White message: A message sent by white process
Every white process takes its snapshot at its convenience, but no later than the instant it receives a red message.
Marker informs process $p_j$ of ${ send(m_{ij}) \,|\, send(m_{ij}) \in LS_i}$
- Every white process records a history of all white messages sent or received by it along each channel.
- When a process turns red, the marker includes these histories along with its snapshot to the initiator process
- The initiator process evaluates $transit(LS_i, LS_j)$ to compute state of $C_{ij}$